As we saw earlier, Hartley transform based fixed pre-processing is
inferior to that based on Fourier transform. An explanation was given
on the basis of symmetries and shift invariance in the section
. Therefore we expect improved performances from Fourier
transform even when the pre-processing is adaptive. However a training
procedure which preserves the symmetries of weight distributions must
be used. Main argument of the use of Hartley transform is to avoid the
complex weights. But as seen from fig., even Fourier
transform can be implemented as a neural network containing real
weights, but with a slightly modified network structure than the usual
MLP. We can easily derive the equations which give the forward and
backward pass.
Forward pass is given by,
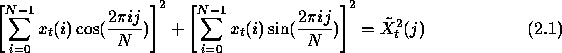
where N denotes the window length, and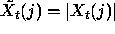 
.
If we use the notation
and error is
denoted by J, then we can find
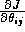simply by using the
chain rule,
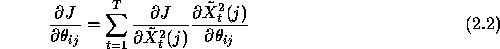
We assume that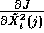 
is known
and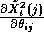 
can simply
be found by differentiating eqn.2.1 wrt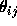 
. Thus we
get,
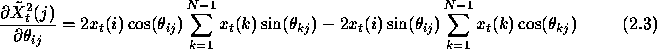
Eqns.2.2 and 2.3 define the backward pass. Note that
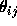can be further back propagated as usual.
