Definition of Hidden Markov Model


Next: Assumptions in the theory
Up: Hidden Markov Models
Previous: Introduction
The Hidden Markov Model is a finite set of states, each of which is
associated with a (generally multidimensional) probability distribution
[]. Transitions among the states are governed by a set of probabilities
called transition probabilities. In a particular state an
outcome or observation can be generated, according to the
associated probability distribution. It is only the outcome, not the
state visible to an external observer and therefore states are
``hidden'' to the outside; hence the name Hidden Markov Model.
In order to define an HMM completely, following elements are needed.
- The number of states of the model, N.
- The number of observation symbols in the alphabet, M. If the
observations are continuous then M is infinite.
- A set of state transition probabilities
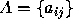 .
.
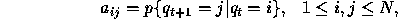
where
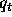 denotes the current state.
denotes the current state.
Transition probabilities should satisfy the normal stochastic
constraints,
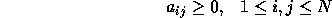
and
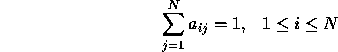
- A probability distribution in each of the
states,
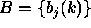 .
.
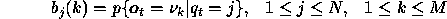
where 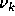 denotes the
denotes the 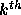 observation symbol in the
alphabet, and
observation symbol in the
alphabet, and 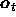 the current parameter vector.
the current parameter vector.
Following stochastic constraints must be satisfied.
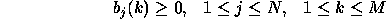
and
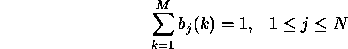
If the observations are continuous then we will have to use a
continuous probability density function, instead of a set of discrete
probabilities. In this case we specify the parameters of the
probability density function. Usually the probability density
is approximated by a weighted sum of M Gaussian distributions  ,
,
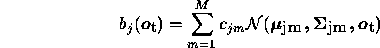
where,
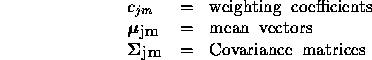
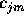 should satisfy the stochastic constrains,
should satisfy the stochastic constrains,
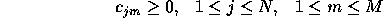
and
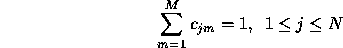
- The initial state distribution,
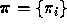 .
.
where,
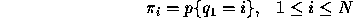
Therefore we can use the compact notation

to
denote an HMM with discrete probability distributions, while
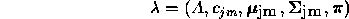
to denote one
with continuous densities.
.
Narada Warakagoda
Fri May 10 20:35:10 MET DST 1996
Home Page
![]()
![]() denotes the current state.
denotes the current state.![]()
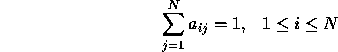
![]()
![]() denotes the
denotes the ![]() observation symbol in the
alphabet, and
observation symbol in the
alphabet, and ![]() the current parameter vector.
the current parameter vector.![]()
![]()
![]() ,
,
![]()
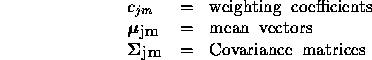
![]() should satisfy the stochastic constrains,
should satisfy the stochastic constrains,
![]()
![]()
![]()